Obscurity.Wiki

👨🏻‍🏫 "Introduction to Complexity" - Unit 2

Table of Contents

#resource/course

📝 Complexity Research

Introduction to Dynamics

Examples:

  • Planetary Dynamics
  • Fluid Dynamics
  • Turbulence Dynamics
  • Electrical Dynamics
  • Climate Dynamics
  • Crowd Dynamics
  • Population Dynamics
  • Financial Dynamics
  • Group Dynamics
  • Social Dynamics (conflict and cooperation)

It's a general field. There are quatitative tools such as differential equations.

Dynamical Systems Theory:

The branch of math for how systems change over time. It gives us vocabulary and tools for describing dynamics It's the attempt to describe general principles regarding systems that change over time using deterministic equations. Universaility in Chaos - Characteristics that are universal across a wide set of chaotic systems. It's these characteristics that may be predictable.

Sub branches:

  • Calculus
  • Diff equations
  • Iterated maps
  • Algebraic topology
  • etc

Notes:

  • So basically, Isaac Newton wanted to understand the dynamics of objects and their movement, which in order to proof his ideas he developed calculus. Or at least that's what I understand so far.
  • What is the difference between chaos and randomness?
  • What's "deterministic chaos"?
  • A model is a simple representation of something in nature

Ideas:

  • Are there predictions that we humans can make that would be impossible or very difficult/power intense for math or algorithms? Does current AI fill this gap? This basically assumes that there is a way to compress the behavior of complex systems into a single model which could fit the observed behavior. But this would not mean that what's observed can fit in a model. What's observed could in fact be infinite or eternal and never able to be captured into a single compressed view.
    • Pierre Simon Laplace quote: Prediction could be possible (wrong) - Pierre Simon Laplace
    • Henri Pincaré quote: Prediction becomes impossible - Henri Pincaré

Chaos in nature (examples):

  • Elecgrical circuits
  • Computer networks
  • Brain activity
  • Climate
  • etc

Logistic Map

  • X_t+1 = R • (X_t - X_t^2)
  • Still unsure about how it is used and why it works
  • Ultimate dynamics
  • Fixed point attractor (dynamics)
  • What's the proof that says that it will always reach a stable fixed point? It doesn't it seems, it can infinetily oscilate between diff states, called periodic attractor.
  • Oscilations can vary on multiple states
  • If growth rate (R) increases it becomes harder to predict what the state will be later on. This is called "Chaos".
  • Prediction becomes impossible with different initial values of X_t
  • Bifurcation Diagram Bifurcation Diagram
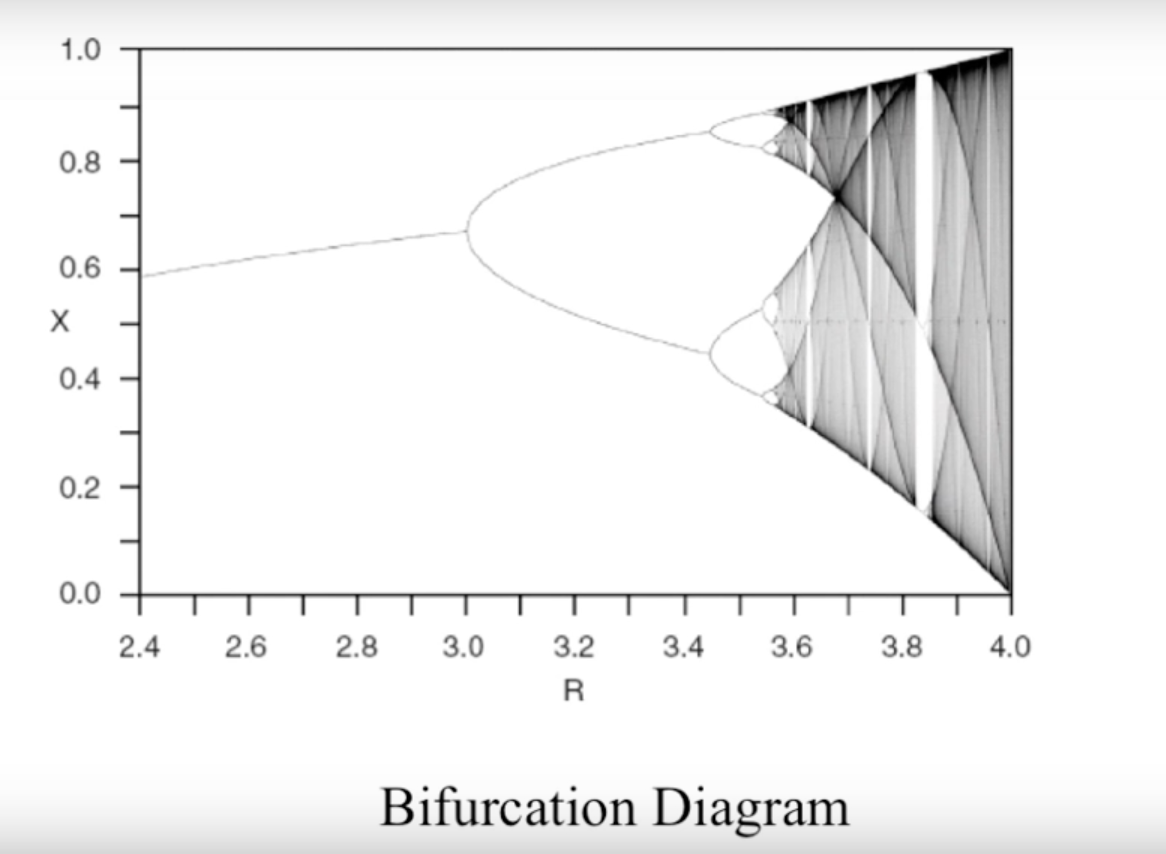
  • "Onset of chaos" (3.569946...) is the value of growth rate (R) that produces an infinite set of states in which the population oscillates.
  • Feigenbaum's universal constant ~= 4.6692016... which stands for the acceleration in which chaos grows

Logistic Map Bifurcation Diagram with Notes Showing 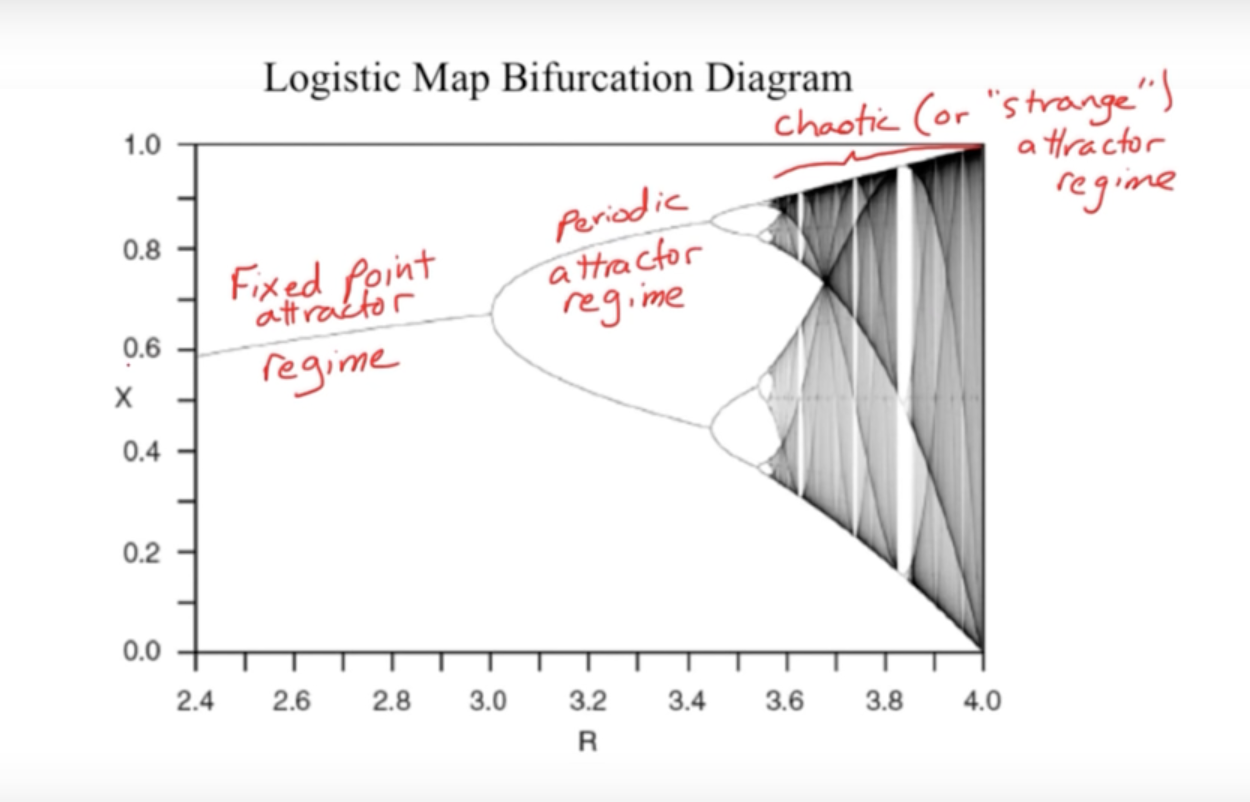Logistic Map Bifurcation Diagram with Notes:

  • Fixed point attractor regime
  • Periodic attractor regime
  • Chaotic or "Strange" attractor regime

There are "Unibody maps" or "one-humped maps" like the Logistic Map. They all share some universalities like Feigenbaum's universal constant and the eventual rise to chaos.